数据对象与属性类型
数据集由数据对象组成。一个数据对象代表一个实体。例如销售数据库中,对象可以是顾客、商品。属性是一个数据字段,表示数据对象的一个特征。
属性类型
标称属性(nominal attribute):一些事物的名称,每个值代表某种类别、编码或者状态。不具有有意义的序,不是定量的,其均值和中位数无意义,总数有意义。例如,颜色这个对象的属性可能有黑色、红色、白色等,职业可能值有教师、医生等。
二元属性(binary attribute):一种标称属性,只有两个类别或状态:0或1。有对称和非对称两种情况,对称比如性别男女两种状态;非对称比如HIV检测中的阳性和阴性,为了方便,通常用1表示最重要的结果(通常是稀有的,另一个用0编码。
序数属性(ordinal attribute):值之间具有有意义的序,但是相继值之间的差未知。其中心趋势可以用众数和中位数来表示,但不能定义均值。比如成绩有A+、A、A-等。
上面三个都是定性的属性,即它们描述对象的特征而不给出实际大小或数量,其值只代表编码,而不是可测量的量。
- 数值属性(numeric attribute)是定量的,可度量,用整数或实数值表示。
- 区间标度属性(interval-scaled):允许比较和定量评估值之间的差,但是没有真正的零点,没有比率或者倍数关系,可以计算中位数,众数和均值。例如,摄氏温度,我们不能说10摄氏度比5摄氏度温暖2倍。
- 比率标度属性(ratio-scaled):具有固定零点,可以计算均值、中位数和众数。例如,工作年限、文章字数等计数属性。
数据的基本统计描述
我们为了把握数据的全貌,关注数据的中心趋势度量、数据的散布和图形显示。
中心趋势度量
中心趋势度量度量数据分布的中部或中心位置,或者说,给定一个属性,它的值大部分落在何处?
均值 (mean)
最常用最有效的是的算术均值:
$$ \overline{x} = \frac{\sum_{i=1}^N x_i}{N} $$
或者使用加权平均,反映对应值的意义、重要性或者出现频率。
$$ \overline{x} = \frac{\sum_{i=1}^N w_ix_i}{\sum_{i=1}^N w_i} $$
但是均值对极端值很敏感,对于非对称数据,数据中心更好的度量是中位数。
中位数 (median)
中位数是有序数据的中间值,将数据分成两半。
中位数在观测数量很大时,计算开销很大。下面给出近似计算公式。假定数据根据值划分成了区间,并且已知每个区间的频率(数据值的个数)。令包含中位数频率的区间为中位数区间。
其中,$L_1$是中位数区间下界,$N$是整个数据集中值的个数,$\sum freq$是低于中位数区间的所有区间的频率和,$freq_{median}$是中位数区间的频率,$width$是中位数区间的宽度。
众数 (mode)
出现最频繁的值。具有有一个、两个、三个众数的数据集合分别成为单峰的(unimodal)、双峰的(bimodal)、三峰的(trimodal)。
当数据对称时,众数 = 中位数 = 均值。
当次数分布右偏时,即正倾斜时,均值受偏高数值影响较大,其位置必然在众数之右,中位数在众数与算术平均数之间,众数 < 中位数 < 均值。
反之,当次数分布左偏时,即负倾斜时,均值受偏小数值的影响较大,其位置在众数之左,中位数仍在两者之间,均值 < 中位数 < 众数。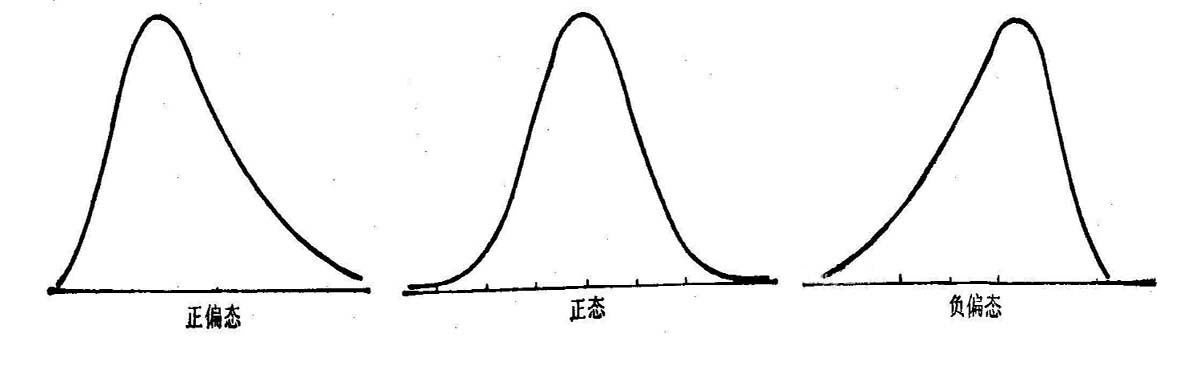
中列数(midrange)
最大和最小值的平均值。
数据的散布
极差(range)
最大值和最小值之差。
四分位数(quartile)
把数据划分成四个基本上大小相等的连贯集合。
$ Q_1 $:有25%的数据在此之下;
$ Q_2 $:有50%的数据在此之下,即中位数;
$ Q_3 $:有75%的数据在此之下。
四分位数极差IQR:给出被数据中间一半所覆盖的范围。
$$ IQR = Q_3 - Q_1 $$
对于倾斜分布,单个散步数值度量如IQR都不是很有用,识别可以离群点的通常规则是挑选落在 $Q_3$ 之上和 $Q_1$ 之下至少 $1.5 * IQR$ 处的值。
五数概括:最小值、$Q_1$、中位数、$Q_3$、最大值。盒图体现了五数概括。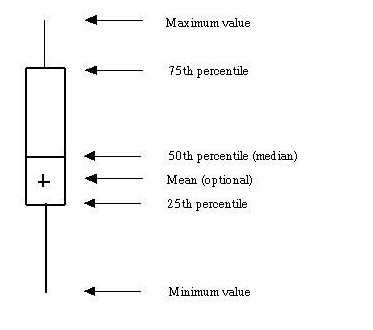
方差(Variance)和标准差(Standard deviation)
$$ \sigma ^2 = \frac{1}{N} \sum_{i=1}^{N}(x_i - \overline{x})^2 $$
$\sigma ^2$ 是方差,$\sigma$是标准差。
图形显示
分位数图
设 $x_i$ 是按递增顺序的数据,使得 $x_1$ 是最小的观测值,而 $x_N$ 是最大的,每个观测值$x_i$ 与一个百分数$f_i$对应,指出大约$f_i * 100%$的数据小于值$x_i$。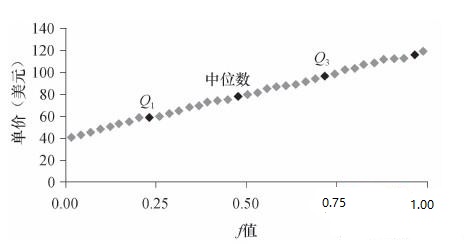
分位数-分位数图
可以使得用户观察从一个分布到另一个分布是否有漂移。
例如两个部门销售商品的单价数据的分位数-分位数图。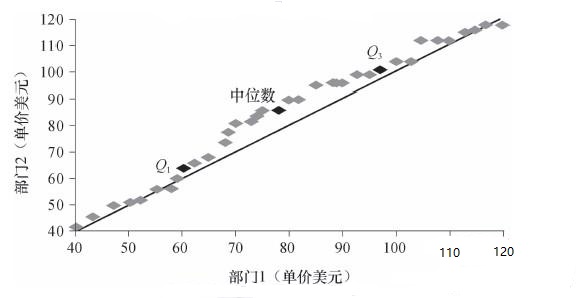
比如在$Q2$,部门1销售的商品50%低于或等于78美元,而部门21销售的商品50%低于或等于85美元。中间那条45度实线代表没有偏移。从总体来看也可以看出部门1销售的商品单价趋向于比部门2低。
(频率)直方图
如果数据是标称的,一般称作条形图,数据是数值的,多使用术语直方图。
散点图
散点图是一种观察双变量数据的有用方法。可以通过其看出两个变量是正相关、负相关还是不相关的。
度量数据的相似性和相异性
相似性和相异行都称为邻近性,用于评估对象之间相互比较的相似或不相似的程度。
数据矩阵和相异性矩阵
数据矩阵
n个对象被p个属性刻画。
对象-属性结构,行代表对象,列代表属性,因此数据矩阵通常被称为二模矩阵。
$$
\left[
\begin{matrix}
x_{11} & \cdots & x_{1f} & \cdots & x_{1p} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
x_{i1} & \cdots & x_{if} & \cdots & x_{ip} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
x_{n1} & \cdots & x_{nf} & \cdots & x_{np}
\end{matrix}
\right]
$$
相异性矩阵
存放n个对象两两之间的邻近度。
对象-对象结构,只包含一类实体,因此被称为单模矩阵。
$$
\left[
\begin{matrix}
0 & & & & \\
d(2,1) & 0 & & & \\
d(3,1) & d(3,2) & 0 & & \\
\vdots & \vdots & \vdots & & \\
d(n,1) & d(n,2) & \cdots & \cdots & 0
\end{matrix}
\right]
$$
该矩阵是对称的,$d(i,j)$是对象i和对象j之间的相异性的度量,其中$d(i,i) = 0$,即一个对象与自己的差别为0。
下面我们讨论对于不同类型数据的邻近性度量方法。
标称数据的邻近性度量
标称属性可以取不同的状态,如颜色有红、黄等状态,这些状态可以用字母、符号或者一组整数来表示。
两个对象之间的相异性可以根据不匹配率来计算。
$$d(i,j) = \frac{p-m}{p} $$
其中,m是匹配的数目,即i和j取值相同状态的属性数,p是属性总数。
相似性可以根据下式计算:
$$ sim(i,j) = 1 - d(i, j) = \frac{m}{p} $$
标称属性可以使用非对称的二元属性编码,如对颜色,可以对所有的颜色状态分别创建一个二元变量,如果一个对象为黄色,则黄色属性设置为1,其他设置为0。
二元属性的邻近性度量
| 1 | 0 | |
|---|---|---|
| 1 | q | r |
| 0 | s | t |
在上表中,q是对象i和j都取1的属性数,其他类似。
对于对称的二元属性:
$$ d(i,j) = \frac{r+s}{q+r+s+t} $$
对于非对称的二元树型,一般两个值都取1被认为比两个都取0的情况更有意义,负匹配数t通常忽略。
$$ d(i,j) = \frac{r+s}{q+r+s} $$
非对称的二元相似性被称为Jaccard系数,在文献中被广泛使用。
$$ sim(i,j) = \frac{q}{q+r+s} = 1 - d(i,j) $$
数值属性的相异性:闵科夫斯基距离
$$
d(i,j) = \sqrt[h]{|x_{i1} - x_{j1}|^h + \cdots + |x_{ip} - x_{jp}|^h}
$$
当h=1时,为曼哈顿距离,$ d(i,j) = |x_{i1} - x_{j1}| + \cdots + |x_{ip} - x_{jp}|$
当h=2时,为欧几里得距离,$ d(i,j) = \sqrt[2]{|x_{i1} - x_{j1}|^2 + \cdots + |x_{ip} - x_{jp}|^2} $
当h趋近于无穷时,为上确界距离,即两个对象的最大属性值差,$ d(i,j) = \max_{f}^{p}|x_{if}-x_{jf}| $
序数属性的邻近性度量
- 假设$f$为一个序数属性,值为$x_{if}$,其有$M_f$个有序的状态,表示排位,用对应的排位$r_{if} \in {1,\dots,M_F}$取代$x_{if}$
- 由于每个序数属性都可能有不同的状态数,所以通常将每个属性的值域映射到$[0.0,1.0]$上,用$z_{if}$代替$r_{if}$来实现数据规格化。
$$ z_{if} = \frac{r_{if}-1}{M_{f}-1} $$ - 这时候序数属性的邻近性度量就可以转换为数值属性的邻近性度量来求了。
混合属性的相异性
一个对象可能包含很多不同类型的数据,可能有标称的、对称或者非对称二元的、数值的或者序数的,假设数据集包含$ p $个混合类型的属性,则:
$$
d(i,j) = \frac{ \sum_{f=1}^{p} \delta_{ij}^{[f]} d_{ij}^{[f]} } { \sum_{f=1}^{p} \delta_{ij}^{[f]} }
$$
其中,如果对象i和对象j没有属性f的度量值,或者两个对象的f的度量值都为0且f是非对称的二元属性,则$\delta_{ij}^{[f]}=0$,否则取1。
至于$d_{ij}^{[f]}$,
- f是数值的:$ d_{ij}^{[f]} = \frac{|x_{if}-x_{jf}|} {\max_{h} x_{hf}-\min_{h} x_{hf}} $ ,其中,h遍取属性f的所有非缺失对象。
- f是标称或二元的:如果$x_{if} = x_{jf}$,则$d_{ij}^{[f]}=0$,否则取1。
- f是序数的:计算排位$r_{if}$和$z_{if} = \frac{r_{if}-1}{M_f-1}$,然后作为数值属性处理。
余弦相似性
用来比较文档,每个文档都被一个所谓的词频向量表示,通常很长,而且稀疏,传统的距离度量效果并不好。
$$ sim(i,j) = \frac{x \cdot y}{||x|| ||y||} $$
当属性是二值属性时,$x \cdot y$是$x$ 和$y$共有的属性数,而$|x||y|$是$x$具有的属性数 和$y$具有的属性数的几何均值,于是$sim(x,y)$是公共属性相对拥有的一种度量,余弦相似性一个简单变种如下:
$$
sim(x,y) = \frac{x \cdot y}{x \cdot x + y \cdot y - x \cdot y}
$$
称为Tanimoto距离,常用在信息检索和生物学分类中。